Hogeschool IPABO > Comenius > Leren van een les
Leren van een les
In deze les maken leerlingen uit groep 7 een grafiek van de groei van een zonnebloem. Ze leren dat zowel een staafgrafiek als een lijngrafiek geschikt is. Ze ontdekken dat een lijngrafiek ook laat zien hoe de groei tussen de metingen waarschijnlijk is verlopen.
Link naar de les op de website van Volgens Bartjens.

Vragen met als doel de hele les en de video’s in samenhang te doordenken:
Vooraf:
Iemand wilde wekelijks de lengte van een zonnebloem meten, maar uiteindelijk kwam daar niet veel van terecht. De tabel toont de verzamelde gegevens.
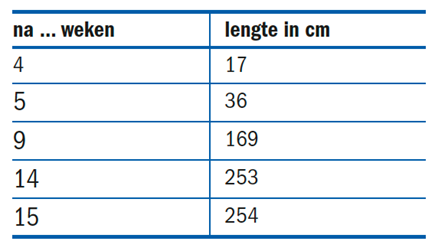
- Teken een grafiek bij de gegevens.
- Welke grafieken verwacht je van de leerlingen? Maak een voorspelling.
- Welke voorkennis hebben ze nodig om een grafiek te kunnen tekenen?
- Lees het lesplan. Waar ben je nieuwsgierig naar als je straks de video’s van deze les gaat bekijken?
Tijdens het bekijken van de video’s:
Video 1: Een gesprek over zonnebloemen en over de vraag hoe je de groei ervan in beeld kunt brengen.
- Hoe stimuleert de leerkracht de nieuwsgierigheid van de leerlingen tijdens de introductie?
- Hoe activeert de leerkracht de voorkennis van de leerlingen over grafieken?
Video 2: De tabel met de metingen. De lengte is niet elke week gemeten.
- Op welke manier moedigt de leerkracht de leerlingen aan om kritisch naar de meetgegevens in de tabel te kijken?
- Waarom denk je dat de leerkracht heeft gekozen voor de opbouw: eerst een schets maken, dan overleggen met een maatje, en daarna samen een nette grafiek maken?
Video 3: Een bespreking tussendoor.
- Wat doet de leerkracht om leerlingen kritisch te laten nadenken over wat er wel en niet klopt aan de getoonde schetsen?
- Hoe begeleidt de leerkracht de leerlingen bij het bedenken van een manier om de groei in de weken zonder meetgegevens toch in beeld te brengen?
Video 4: Gesprek met twee leerlingen en nog een tweede bespreking tussendoor.
- Hoe reageert de leerkracht op de signalen dat leerlingen moeite hebben met de schaalverdeling op de assen?
Video 5: Gesprek met twee andere leerlingen. De leerlingen krijgen de opdracht elkaars grafieken te bekijken.
- Welke misvattingen of onduidelijkheden komen in dit fragment naar voren?
Video 6: Bespreking. De leerkracht vertelt wat zij van de les heeft geleerd.
- Waarom zou de leerkracht ervoor kiezen om de nabespreking te beginnen met wat ze zelf heeft geleerd?
- Hoe laten leerlingen zien dat ze inzicht hebben in wat een grafiek correct of incorrect maakt, en kunnen ze dit met argumenten onderbouwen?
Video 7: Terugblik na de les.
- In hoeverre herken je de punten die de leerkracht benoemt tijdens haar terugblik? Benoemt zij ook inzichten of aandachtspunten die jou zelf nog niet waren opgevallen?
- Wat vind je van de conclusie van de leerkracht dat er meer aandacht moet komen voor het tekenen van grafieken in plaats van alleen het aflezen? Herken je dit als een belangrijk aandachtspunt?
Als je deze les zelf wilt geven:
- Hoe heeft de leerkracht zich waarschijnlijk op de les voorbereid?
- Wat zou je daarvan willen overnemen en wat zou je anders doen?
- Wat zijn de leerdoelen voor jezelf?
Verdere theoretische verdieping:
Vaktaal:
Om de les goed te analyseren, is vaktaal essentieel. Leg in je eigen woorden uit hoe de onderstaande vaktaalwoorden in de les naar voren komen. Welke nieuwe inzichten heb je gekregen ten aanzien van deze woorden? De lijst is niet uitputtend; voeg zelf andere relevante begrippen toe die je kunt gebruiken om de les te analyseren.
- Continu
- Discreet
- Interpoleren
- Lijngrafiek
- Schaal
- Staafgrafiek
- Reflectie
- Reprenteren
- Verhouding
- Wiskundig modelleren
- Wiskundige attitude
- …
Literatuursuggesties:
In de video-opnamen heb je gezien dat het zelf tekenen van een grafiek voor veel leerlingen nog best lastig is. Meer hierover lees je in hoofdstuk 11 van Kerninzichten, hoofdstuk 7 van Rekenen met verhoudingen op de basisschool, In het artikel van Keijzer en Van Galen wordt beschreven waarom het zo belangrijk is dat leerlingen zelf grafieken leren tekenen omdat ze dan pas gaan begrijpen hoe grafieken in elkaar zitten.
- Keijzer, R., & Van Galen, F. (2014). De kunst van het weglaten. Volgens Bartjens, 34(1), 32-35.
- Oonk, W., Keijzer, R., Lit, S., Barth, F., den Engelsen, M., Lek, A., & Van Waveren Hogervorst, C. (2023). Wiskunde in de praktijk. Kerninzichten (4e druk). Noordhoff Uitgevers.
- Van Galen, F., & Markusse, A. (2023). Rekenen met verhoudingen op de basisschool (2e druk). Noordhoff Uitgevers.
- Van Galen, F., Leszijnski, T. (2025). Leren van een les. Volgens Bartjens, 45(1), 8-9.
