Link naar de les op de website van Volgens Bartjens.

Vragen met als doel de hele les en de video’s in samenhang te doordenken:

Vooraf:

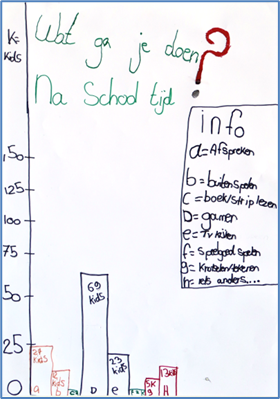
Er is een onderzoekje uitgevoerd onder 150 leerlingen van groep 7 en 8 over de vraag wat ze het liefst deden als ze uit school komen. In de laatste kolom van de onderstaande tabel zie je wat deze leerlingen hebben opgegeven. De 26 leerlingen uit de klas van Tamara hebben het onderzoekje ook in de eigen groep uitgevoerd. Hun gegevens staan in de voorlaatste kolom.

• Teken een grafiek bij de gegevens.
• Welke grafieken verwacht je van de leerlingen? Maak een voorspelling.
• Welke voorkennis hebben ze nodig om een grafiek te kunnen tekenen?
• Lees het lesplan. Waar ben je nieuwsgierig naar als je straks de video’s van deze les gaat bekijken?

Tijdens het bekijken van de video’s:

Video 1: Introductie

• Hoe zorgt de leerkracht ervoor dat de leerlingen begrijpen wat het probleem is?
• Hoe blijkt uit de uitspraken van leerlingen welke voorkennis zij over grafieken hebben?

Video 2: Uitwisseling van eerste ideeën

• Hoe maakt de leerkracht ruimte voor gezamenlijke probleemverkenning in het gesprek met leerlingen?
• Welke misvattingen of onduidelijkheden komen naar voren over de schaalverdeling en de lengte van de verticale as?
• Hoe stimuleert de leerkracht dat leerlingen reageren op elkaars vragen of opmerkingen?

Video 3: Presentatie en afsluiting

• Hoe reageren leerlingen op de grafiekpresentatie: welke tops en tips worden gegeven, en hoe constructief zijn die?
• Hoe verwoorden leerlingen wat ze moeilijk vonden en wat ze anders willen doen?
• Hoe zichtbaar is de betrokkenheid van leerlingen bij het gesprek na de presentatie?
• Hoe neemt de leerkracht de rol van gespreksleider op zich, terwijl zij het eigenaarschap bij de leerlingen laat?

Video 4: Leerlingen reageren op foute grafieken

• In hoeverre herkennen leerlingen de gemaakte fouten in de grafieken, en kunnen ze uitleggen waarom iets niet klopt?
• Wat doet de leerkracht om het geven van kritiek op fouten (ook van haarzelf) normaal en waardevol te maken?
• Hoe draagt de manier waarop de klas is ingericht en het zitten rondom het bord bij aan het groepsgevoel en de betrokkenheid in het gesprek?

Video 5: Impressie van het zelfstandig werken en afsluiting

• Hoe wordt zichtbaar dat leerlingen zich bewuster worden van het belang van een correcte asindeling in een grafiek?

Als je deze les zelf wilt geven:

• Hoe heeft de leerkracht zich waarschijnlijk op de les voorbereid?
• Wat zou je daarvan willen overnemen en wat zou je anders doen?
• Wat zijn de leerdoelen voor jezelf?

Verdere theoretische verdieping:

Vaktaal:

Om de les goed te analyseren, is vaktaal essentieel. Leg in je eigen woorden uit hoe de onderstaande vaktaalwoorden in de les naar voren komen. Welke nieuwe inzichten heb je gekregen ten aanzien van deze woorden? De lijst is niet uitputtend; voeg zelf andere relevante begrippen toe die je kunt gebruiken om de les te analyseren.

• Continu
• Discreet
• Schaal
• Staafgrafiek
• Reflectie
• Reprenteren
• Verhouding
• Wiskundig modelleren
• Wiskundige attitude
• …

Literatuursuggesties:

In de video-opnamen heb je gezien dat het zelf tekenen van een grafiek voor veel leerlingen nog best lastig is. Meer hierover lees je in hoofdstuk 11 van Kerninzichten, hoofdstuk 7 van Rekenen met verhoudingen op de basisschool, In het artikel van Keijzer en Van Galen wordt beschreven waarom het zo belangrijk is dat zelf grafieken leren tekenen omdat ze dan pas gaan begrijpen hoe grafieken in elkaar zitten.

• Keijzer, R., & Van Galen, F. (2014). De kunst van het weglaten. Volgens Bartjens, 34(1), 32-35.
• Oonk, W., Keijzer, R., Lit, S., Barth, F., den Engelsen, M., Lek, A., & Van Waveren Hogervorst, C. (2023). Wiskunde in de praktijk. Kerninzichten (4e druk). Noordhoff Uitgevers.​
• Van Galen, F., & Markusse, A. (2023). Rekenen met verhoudingen op de basisschool (2e druk). Noordhoff Uitgevers.
• Van Galen, F., Leszijnski, T. (2022). Puzzelen. Volgens Bartjens, 41(5), 8-10.